Neural Network making Predictions - Part 1 - DevInDeep using C# Tutorial

Hello guys and welcome to the first part of the “Neural Networks making Predictions” series.

Today we will talk about the Forward Propagation algorithm. In other words, this is the part of the network that makes the predictions.

Table of Contents

ML.NET Tutorial Series

https://code-ai.mk/introduction-to-machine-learning-in-c-with-ml-net

Neural Networks making Predictions with single input

Now imagine the following scenario:

We are playing a team game. Each team can have up to 10 players. Therefore, the outcome of the game is highly correlated to the number of players on the field.

Now let’s make a prediction using the following code:

double input = 9; 
double weight = 0.1;
double prediction = input * weight;
Console.WriteLine($"Number of players on team: {input}");
Console.WriteLine($"Prediction: {prediction}");

Output:

Making Neural Network Predictions — *Image 1: Making predictions*

This calculation visually can be represented as:

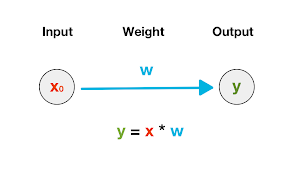
Visual Representation of One Neuron Network — *Image 2: Visual Representation of Prediction Function*

All this means is that a team with 9 players has 90% chance for a win. In other words, the lower the number of players, the lower the chance for a win. A team that is complete (has 10 players on the field), would be translated into a 100% chance for a win.

We programmed a code block, that makes correlation between number of players (input) and the chance for a win (output).

So what about the weight parameter?

Well in our case it measures the sensitivity between the input and output. It’s our knowledge on the given input. This parameter can bring down the importance of the input value. But also increase it. In other words, the more important the input is, the bigger the weight value will be.

A weight decides how much influence the input will have on the output. Even though we only showed a positive number example, we can also predict negative numbers and even take negative numbers as input.

This prediction is based on one input (number of players on the field). But can we make an informed decision relaying only on this factor?

Making prediction with multiple inputs

Is the number of players on the field really a good predictor for the outcome of the game? Well I don’t think so. In order to make better predictions we need more data. So what if we give the prediction function an input that consists of more than one data point? In theory the function should make more accurate predictions.

Let’s introduce the “average years of experience” and “win/loss record” variables.

double numberOfPlayersOnTeam = 9; 
double avgYearsOfExperience = 7.2;
double winLossRecord = 0.85;

double weight1 = 0.033;  
double weight2 = 0.007;  
double weight3 = 0.6;   
double prediction = (numberOfPlayersOnTeam * weight1) + (avgYearsOfExperience * weight2) + (winLossRecord * weight3);
            
Console.WriteLine($"Number of players on team: {numberOfPlayersOnTeam}");
Console.WriteLine($"Average Years of Experience: {avgYearsOfExperience}");
Console.WriteLine($"Win/Loss Record: {winLossRecord}");
Console.WriteLine($"Prediction: {prediction}");

Let’s look at the output:

*Image 3: Making predictions using multiple inputs*

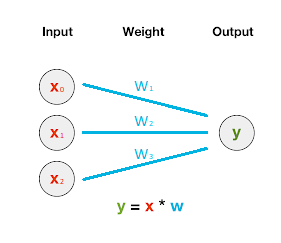
Visual Representation of Prediction Function using multiple inputs — *Imag*e 4: Visual Representation of Prediction Function with multiple inputs

So this neural network is capable to work with multiple inputs at a time per prediction. This allows us to combine various forms of information to make better informed predictions.

But as we can see, nothing has really changed. We have a weight or sensitivity variable for each input. We can see that different input variables are connected to different weight. This is because certain input variables are more valuable then others.

For example, if we put in a variable called “number of fans”, how much impact would that be to the outcome of the game? Would that even matter? And if so, then by how much?

Just by looking at the code, we can see that the variable that makes the most impact on the output is “win/loss record”. But why? Because the respective weight is a lot bigger than the others. So what does that mean? It means that the higher the win/loss record for the team is, the higher is the chance for a win.

Side Note:

Even though we are talking about percentage, the number calculated in the output is not a real percentage. We will see how to convert the output number in a real percentage when we will introduce activation functions

So what about the other variables, do they matter? Well yes, but not as much as the “win/loss record”. The second input variable the matters the most is the “number of players”. Least important is “years of experience”. We can spot this, by looking at the value for the respective weight variable for the input. The higher the weight value is, the higher is the impact on the outcome.

Introducing the “Dot Product”

We are at a point where we need to introduce a little bit of math.

If you have any trouble with this term, then please check the following article. You can find a bunch of examples there.

Or you can check Khaan Academy tutorial

In order to have a bit more intuitive representation of the data we are going to use vector. Vector is nothing more than a list of numbers. In our example we have two vectors. We have input vector, and weights vector.

Since we are multiplying each number based on its position and then summing the results, as it turns out, that’s called dot product.

Now let’s go in and refactor our code to use vector math.

double[] inputVector = { 9, 7.2, 0.85 };
double[] weightsVector = { 0.033, 0.007, 0.6 };
double prediction = dotProduct(inputVector, weightsVector);

Console.WriteLine($"Number of players on team: {inputVector[0]}");
Console.WriteLine($"Average Years of Experience: {inputVector[1]}");
Console.WriteLine($"Win/Loss Record: {inputVector[2]}");
Console.WriteLine($"Prediction: {prediction}");

And the function to calculate the dot product:

private static double dotProduct(double[] input, double[] weights)
{
    double prediction = 0;
    for (int i = 0; i < input.Length; i++)
    {
        prediction += input[i] * weights[i];
    }
    return prediction;
}

This is it for now…

This is only part 1 of “Neural Networks making Predictions” tutorial series. Next we will see how to work with multiple outputs.

Join me in the next part where we are going to investigate some more complex scenarios.

You can download the complete project here.