Discover groups with K-Means in C# with source code.

Source Code Link: Discover Groups – NBA Player Position

Problem Description

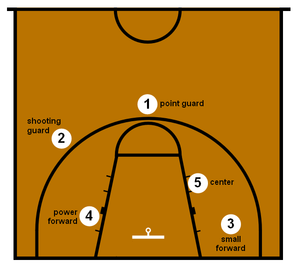
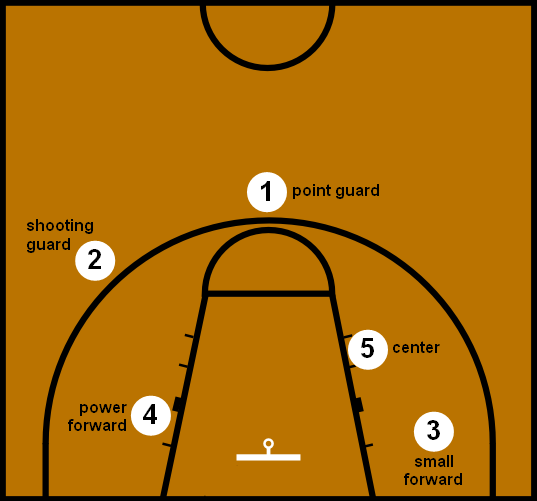
In today’s post we are going to see if we can group modern NBA players into five groups:

• Point guard
• Shooting guard
• Small forward
• Power forward
• Center

Basketball positions – Wikipedia

Discover Groups with K-Means

One of the biggest advantages with K-Means, is given a predefined data set with players data, we can use it to find underlying groups and patterns.

As a result, these underlying groups and patterns will show us how many clusters/groups are there in the data. If we believe that the traditional five position system accurately describes the players skill, we should be able to observe 5 different clusters of players.

In other words, we will find out if modern NBA players skill set can be grouped into five categories on the court.

So, because K-Means is an unsupervised clustering algorithm it fits perfectly into our scenario.

However, if you need a refresher on K-Means algorithm you can check one of the following articles:

• Article Classification
• Image Segmentation
• Shape Recognition

Code Walkthrough

Before we dive right into implementing the solution, let’s look at the data.

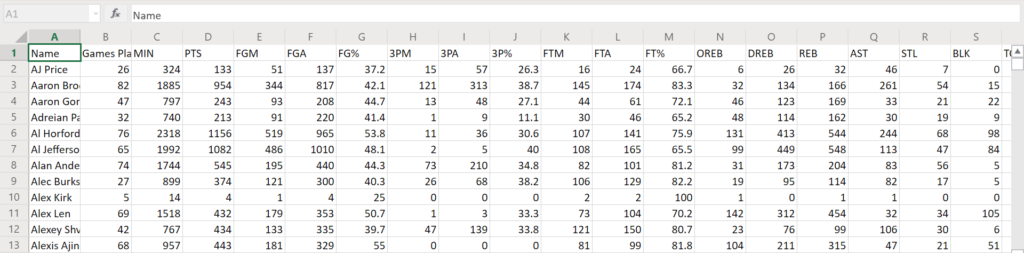
You can find and open the dataset from the project folder: players_stats.csv

First, let’s read in the CSV file

_trainingSet = CSVFile.ImportCSVFileAsList(ofd.FileName, true, ',', 6, 7, 8, 9, 12, 13, 14, 16, 17, 18);s

Here we specify the file path, whether or not to include the header and the field delimiter. You can read more about CSV Files on this link.

In order to find how many groups of players there are, we are going to use the “Elbow Method“.

for (int k = (int)start.Value; k <= (int)end.Value; k++)
{
     List<double[]> distanceResult = new List<double[]>();

     _kMeans = new KMeans(k, eucledeanDistance);
     Centroid[] centroids = _kMeans.Run(_trainingSet.ToArray());

     double result = 0;
     foreach (double[] point in _trainingSet)
     {
          double minValue = Double.MaxValue;
          foreach (Centroid centroid in centroids)
          {
             double distance = eucledeanDistance.Run(point, centroid.Array);
             if (distance < minValue)
                 minValue = distance;
          }
          result += minValue;
      }
      result /= _trainingSet.Count;
      _kmeansPointList.Add(new DPoint(k, result));
}

What we are doing here is, we are running K-Means clustering algorithm for K=1 to K=10. The best K shows us what is the optimal number of clusters for the dataset we are processing.

Results

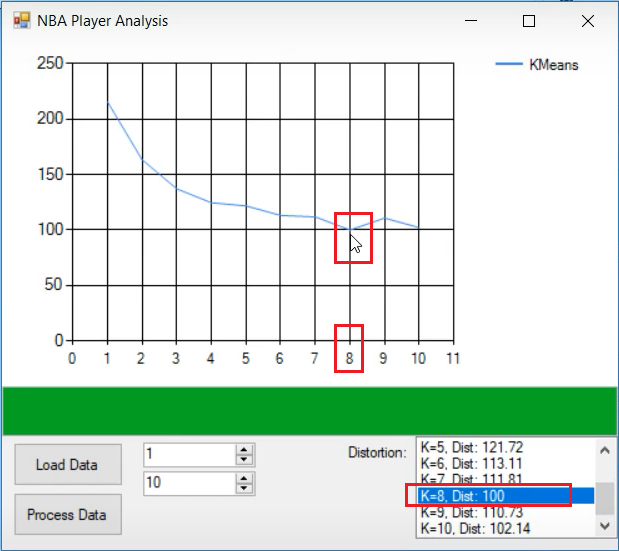
From the image above we can clearly observe that five is not the optimal number of clusters/groups based on the players statistics. Therefore, we can conclude that the traditional five player positions incorrectly oversimplify the skill sets of the modern day NBA players.